Implementing an alternative network sampler

In this tutorial, we demonstrate how to use CORNETO to implement a simple sampler to explore alternative solutions for network inference problems. By perturbing the objective function, we can explore the solution space and identify robust as well as variable components of the network.

We will illustrate this process using a simple example of a network inference problem with CARNIVAL, using the data from the CARNIVAL transcriptomics tutorial.

NOTE: This notebook uses gurobi as the solver and cvxpy as the backend to accelerate the generation of alternative solutions using the warm_start option from cvxpy

import corneto as cn

cn.info()

Installed version: v1.0.0.dev5 (latest stable: v1.0.0-alpha) Available backends: CVXPY v1.6.4, PICOS v2.6.0 Default backend (corneto.opt): CVXPY Installed solvers: CLARABEL, CVXOPT, GLOP, GLPK, GLPK_MI, GUROBI, HIGHS, OSQP, PDLP, PROXQP, SCIP, SCIPY, SCS Graphviz version: v0.20.3 Installed path: /Users/pablorodriguezmier/Documents/work/repos/pablormier/corneto/corneto Repository: https://github.com/saezlab/corneto

from corneto._data import GraphData

# Load dataset from tutorial
dataset = GraphData.load("data/carnival_transcriptomics_dataset.zip")

from corneto.methods.future import CarnivalFlow

m = CarnivalFlow(lambda_reg=0.1)
P = m.build(dataset.graph, dataset.data)
P.objectives

Unreachable vertices for sample: 0

[error_sample1_0: Expression(AFFINE, UNKNOWN, ()),
 multi_sample_regularization_edge_has_signal: Expression(AFFINE, NONNEGATIVE, ())]

# We will sample solutions by perturbing the edge_has_signal variable
P.expr

{'edge_inhibits': edge_inhibits: Variable((3374, 1), edge_inhibits, boolean=True),
 '_dag_layer': _dag_layer: Variable((970, 1), _dag_layer),
 '_flow': _flow: Variable((3374,), _flow),
 'edge_activates': edge_activates: Variable((3374, 1), edge_activates, boolean=True),
 'const0x16b856374e4a9f30': const0x16b856374e4a9f30: Constant(CONSTANT, NONNEGATIVE, (970, 3374)),
 'const0x72fe108f440b0c6': const0x72fe108f440b0c6: Constant(CONSTANT, NONNEGATIVE, (970, 3374)),
 'flow': _flow: Variable((3374,), _flow),
 'vertex_value': Expression(AFFINE, UNKNOWN, (970, 1)),
 'vertex_activated': Expression(AFFINE, NONNEGATIVE, (970, 1)),
 'vertex_inhibited': Expression(AFFINE, NONNEGATIVE, (970, 1)),
 'edge_value': Expression(AFFINE, UNKNOWN, (3374, 1)),
 'edge_has_signal': Expression(AFFINE, NONNEGATIVE, (3374, 1))}

Sampling Solutions Using Random Perturbation

We’ll implement a generic approach to sample alternative solutions by:

1. Introducing small random perturbations to the objective function

2. Re-optimizing the model with these perturbations

3. Collecting solutions that remain close to optimal (within a tolerance threshold)

This technique allows us to explore the space of near-optimal solutions and assess the robustness of different model components.

import numpy as np
import pandas as pd


def sample_alternative_solutions(
    problem,
    target_variable,
    percentage=0.1,
    scale=0.03,
    rel_opt_tol=0.05,
    max_samples=30,
    time_limit=60,
):
    """Sample alternative solutions by perturbing the objective function.

    Parameters:
    -----------
    problem : CORNETO optimization problem
        The optimization problem to sample
    target_variable : variable expression
        The variable to perturb (e.g., P.expr.edge_has_signal or P.expr.vertex_value)
    percentage : float
        Percentage of elements to perturb
    scale : float
        Scale parameter for normal distribution perturbation
    rel_opt_tol : float
        Relative optimality tolerance
    max_samples : int
        Maximum number of samples to generate
    time_limit : int
        Time limit for solver

    Returns:
    --------
    dict : A dictionary containing the results
    """
    # Save the original problem state
    original_problem = problem.solve(solver="gurobi", verbosity=1)

    # Store original objective values
    orig_objectives = []
    for o in problem.objectives:
        print(o.name, o.value)
        orig_objectives.append(o.value)

    # Prepare for perturbation
    shape = target_variable.shape
    num_elements = shape[0]
    n_elements = int(num_elements * percentage)
    vec = np.zeros(shape=num_elements)
    pert = problem.backend.Parameter("perturbation", shape=vec.shape, value=vec)

    # Add perturbation objective
    problem.add_objective(target_variable.T @ pert, name="perturbation")

    # Sample solutions
    selected_edges = []
    edge_values = []
    vertex_values = []

    for i in range(max_samples):
        # Generate random perturbation
        c = np.random.normal(scale=scale, size=n_elements)
        random_indices = np.random.choice(vec.shape[0], size=n_elements, replace=False)
        vec[:] = 0  # Reset vector
        vec[random_indices] = c

        # Update parameter and solve
        pert.value = vec
        solved_problem = problem.solve(
            solver="gurobi",
            warm_start=True,
            ignore_dpp=True,
            TimeLimit=time_limit,
            verbosity=0,
        )
        print(
            f"Sample {i + 1}/{max_samples}: Objective value = {solved_problem.value:.4f}"
        )

        # Check if solution is within tolerance
        accept = True
        for o_orig, o in zip(orig_objectives, problem.objectives):
            if o.name == "perturbation":
                continue
            relative_error = np.abs(o.value - o_orig) / np.abs(o_orig + 1e-10)
            print(f"  {o.name}: {o.value:.4f}, rel error: {relative_error:.4f}")
            if relative_error > rel_opt_tol:
                print(f"  > Rejected! ({relative_error:.4f} >= {rel_opt_tol})")
                accept = False
                break

        if accept:
            selected_edges.append(problem.expr.edge_has_signal.value > 0.5)
            edge_values.append(problem.expr.edge_value.value)
            vertex_values.append(problem.expr.vertex_value.value)

    return {
        "selected_edges": selected_edges,
        "edge_values": edge_values,
        "vertex_values": vertex_values,
    }

Edge-Based Perturbation

First, we’ll sample solutions by perturbing the edge variables. This allows us to explore alternative network topologies where different edges might be selected.

# Create a fresh model
m = CarnivalFlow(lambda_reg=0.1)
P = m.build(dataset.graph, dataset.data)

# Sample solutions by perturbing edge_has_signal
edge_results = sample_alternative_solutions(
    problem=P,
    target_variable=P.expr.edge_has_signal,
    percentage=0.10,
    scale=0.03,
    rel_opt_tol=0.05,
    max_samples=30,
)

# Analyze edge-based results
df_sols = pd.DataFrame(
    np.concatenate(edge_results["selected_edges"], axis=1), index=m.processed_graph.E
).astype(int)
print(f"Generated {df_sols.shape[1]} alternative solutions")
df_sols.head()

Unreachable vertices for sample: 0
===============================================================================
                                     CVXPY                                     
                                     v1.6.4                                    
===============================================================================
(CVXPY) Apr 10 07:10:17 PM: Your problem has 11092 variables, 31652 constraints, and 1 parameters.
(CVXPY) Apr 10 07:10:17 PM: It is compliant with the following grammars: DCP, DQCP
(CVXPY) Apr 10 07:10:17 PM: CVXPY will first compile your problem; then, it will invoke a numerical solver to obtain a solution.
(CVXPY) Apr 10 07:10:17 PM: Your problem is compiled with the CPP canonicalization backend.
-------------------------------------------------------------------------------
                                  Compilation                                  
-------------------------------------------------------------------------------
(CVXPY) Apr 10 07:10:17 PM: Compiling problem (target solver=GUROBI).
(CVXPY) Apr 10 07:10:17 PM: Reduction chain: CvxAttr2Constr -> Qp2SymbolicQp -> QpMatrixStuffing -> GUROBI
(CVXPY) Apr 10 07:10:17 PM: Applying reduction CvxAttr2Constr
(CVXPY) Apr 10 07:10:17 PM: Applying reduction Qp2SymbolicQp
(CVXPY) Apr 10 07:10:17 PM: Applying reduction QpMatrixStuffing
(CVXPY) Apr 10 07:10:17 PM: Applying reduction GUROBI
(CVXPY) Apr 10 07:10:17 PM: Finished problem compilation (took 5.276e-02 seconds).
(CVXPY) Apr 10 07:10:17 PM: (Subsequent compilations of this problem, using the same arguments, should take less time.)
-------------------------------------------------------------------------------
                                Numerical solver                               
-------------------------------------------------------------------------------
(CVXPY) Apr 10 07:10:17 PM: Invoking solver GUROBI  to obtain a solution.
Set parameter Username
Set parameter LicenseID to value 2593994
Academic license - for non-commercial use only - expires 2025-12-02
Set parameter OutputFlag to value 1
Set parameter QCPDual to value 1
Gurobi Optimizer version 12.0.1 build v12.0.1rc0 (mac64[arm] - Darwin 24.4.0 24E248)

CPU model: Apple M4 Pro
Thread count: 12 physical cores, 12 logical processors, using up to 12 threads

Non-default parameters:
QCPDual  1

Optimize a model with 31652 rows, 11092 columns and 111482 nonzeros
Model fingerprint: 0xca949f9c
Variable types: 4344 continuous, 6748 integer (6748 binary)
Coefficient statistics:
  Matrix range     [1e+00, 1e+03]
  Objective range  [1e-01, 8e+00]
  Bounds range     [1e+00, 1e+00]
  RHS range        [1e+00, 1e+03]
Found heuristic solution: objective 0.0000000
Presolve removed 18549 rows and 1627 columns
Presolve time: 0.14s
Presolved: 13103 rows, 9465 columns, 82774 nonzeros
Variable types: 3602 continuous, 5863 integer (5853 binary)

Root relaxation: objective -2.060081e+02, 1253 iterations, 0.02 seconds (0.06 work units)

    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

     0     0 -206.00811    0   69    0.00000 -206.00811      -     -    0s
     0     0 -202.60774    0   71    0.00000 -202.60774      -     -    0s
     0     0 -202.32031    0   65    0.00000 -202.32031      -     -    0s
     0     0 -202.32031    0   60    0.00000 -202.32031      -     -    0s
     0     0 -202.27031    0   59    0.00000 -202.27031      -     -    0s
     0     0 -202.27031    0   47    0.00000 -202.27031      -     -    0s
     0     0 -202.27031    0   51    0.00000 -202.27031      -     -    0s
     0     0 -202.27031    0   51    0.00000 -202.27031      -     -    0s
     0     0 -202.27031    0   14    0.00000 -202.27031      -     -    0s
     0     0 -202.27031    0   45    0.00000 -202.27031      -     -    0s
     0     0 -202.25364    0   34    0.00000 -202.25364      -     -    0s
     0     0 -202.23697    0   55    0.00000 -202.23697      -     -    0s
H    0     0                    -198.0703069 -202.23697  2.10%     -    0s
H    0     0                    -198.9703069 -202.22031  1.63%     -    0s
     0     0 -202.22031    0   35 -198.97031 -202.22031  1.63%     -    0s
     0     0 -202.20364    0   35 -198.97031 -202.20364  1.63%     -    0s
     0     0 -202.15364    0   65 -198.97031 -202.15364  1.60%     -    0s
H    0     0                    -201.7703069 -202.15364  0.19%     -    0s
     0     0 -202.15364    0   67 -201.77031 -202.15364  0.19%     -    0s
     0     0 -202.10364    0   70 -201.77031 -202.10364  0.17%     -    0s
     0     0 -202.10364    0   68 -201.77031 -202.10364  0.17%     -    0s
     0     0 -202.09531    0   58 -201.77031 -202.09531  0.16%     -    0s
     0     0 -202.07031    0   57 -201.77031 -202.07031  0.15%     -    0s
     0     0 -202.07031    0   51 -201.77031 -202.07031  0.15%     -    0s
     0     0 -202.07031    0   53 -201.77031 -202.07031  0.15%     -    0s
     0     0 -202.07031    0   24 -201.77031 -202.07031  0.15%     -    0s
     0     0 -202.07031    0   26 -201.77031 -202.07031  0.15%     -    0s
     0     0 -202.07031    0   25 -201.77031 -202.07031  0.15%     -    0s
     0     0 -202.07031    0   25 -201.77031 -202.07031  0.15%     -    1s
     0     0 -202.07031    0   37 -201.77031 -202.07031  0.15%     -    1s
     0     0 -202.07031    0   37 -201.77031 -202.07031  0.15%     -    1s
     0     0 -202.07031    0   37 -201.77031 -202.07031  0.15%     -    1s
     0     0 -202.07031    0   37 -201.77031 -202.07031  0.15%     -    1s
     0     2 -202.07031    0   37 -201.77031 -202.07031  0.15%     -    1s
H   28    16                    -201.8703069 -201.97031  0.05%  22.7    1s
H   76    38                    -201.9703069 -201.97031  0.00%  17.7    1s

Cutting planes:
  Learned: 2
  Gomory: 5
  Cover: 1
  Implied bound: 26
  Clique: 2
  MIR: 37
  Inf proof: 1
  Zero half: 7
  Mod-K: 2
  RLT: 11
  Relax-and-lift: 6

Explored 93 nodes (8523 simplex iterations) in 1.37 seconds (2.08 work units)
Thread count was 12 (of 12 available processors)

Solution count 6: -201.97 -201.87 -201.77 ... 0
No other solutions better than -201.97

Optimal solution found (tolerance 1.00e-04)
Best objective -2.019703069210e+02, best bound -2.019703069210e+02, gap 0.0000%
-------------------------------------------------------------------------------
                                    Summary                                    
-------------------------------------------------------------------------------
(CVXPY) Apr 10 07:10:19 PM: Problem status: optimal
(CVXPY) Apr 10 07:10:19 PM: Optimal value: 1.622e+01
(CVXPY) Apr 10 07:10:19 PM: Compilation took 5.276e-02 seconds
(CVXPY) Apr 10 07:10:19 PM: Solver (including time spent in interface) took 1.406e+00 seconds
error_sample1_0 7.0169713497161865
multi_sample_regularization_edge_has_signal 92.0
Sample 1/30: Objective value = 15.9878
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 2/30: Objective value = 16.2013
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 3/30: Objective value = 16.2013
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 4/30: Objective value = 16.1317
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 5/30: Objective value = 16.1711
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 6/30: Objective value = 16.2996
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 93.0000, rel error: 0.0109
Sample 7/30: Objective value = 16.2228
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 8/30: Objective value = 16.2558
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 9/30: Objective value = 16.1316
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 10/30: Objective value = 15.8947
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 11/30: Objective value = 16.0179
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 12/30: Objective value = 15.8665
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 13/30: Objective value = 16.1839
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 14/30: Objective value = 16.2407
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 15/30: Objective value = 16.1211
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 16/30: Objective value = 16.0665
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 17/30: Objective value = 15.8804
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 18/30: Objective value = 16.2178
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 19/30: Objective value = 16.0880
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 20/30: Objective value = 16.2337
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 21/30: Objective value = 16.2322
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 22/30: Objective value = 15.8936
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 23/30: Objective value = 16.1274
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 24/30: Objective value = 16.0623
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 25/30: Objective value = 15.9696
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 93.0000, rel error: 0.0109
Sample 26/30: Objective value = 16.0228
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 27/30: Objective value = 15.9609
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 28/30: Objective value = 16.1027
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 29/30: Objective value = 16.2100
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 30/30: Objective value = 16.1709
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Generated 30 alternative solutions

		0	1	2	3	4	5	6	7	8	9	...	20	21	22	23	24	25	26	27	28	29
(SMAD3)	(MYOD1)	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
(GRK2)	(BDKRB2)	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
(MAPK14)	(MAPKAPK2)	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
(DEPTOR_EEF1A1_MLST8_MTOR_PRR5_RICTOR)	(FBXW8)	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
(SLK)	(MAP3K5)	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0

5 rows × 30 columns

# Analyze variability in edge selection
df_var = pd.concat([df_sols.mean(axis=1), df_sols.std(axis=1)], axis=1)
df_var.columns = ["mean", "std"]
print("Edges with highest variability across solutions:")
df_var.sort_values(by="std", ascending=False).head(50).sort_values(by="mean")

Edges with highest variability across solutions:

		mean	std
(PPP2CA)	(RB1)	0.300000	0.466092
(PML)	(SMAD3)	0.300000	0.466092
(MAPK1)	(JUN)	0.300000	0.466092
(GSK3B)	(NFKB1_RELA)	0.300000	0.466092
(MAPK3)	(PML)	0.333333	0.479463
(CTNNB1)	(KLF4)	0.333333	0.479463
(PHLPP1)	(STK4)	0.333333	0.479463
(GSK3B)	(CDKN1A)	0.366667	0.490133
(MAPK3)	(GSK3B)	0.366667	0.490133
(APC_AXIN1_GSK3B)	(ROR2)	0.400000	0.498273
(RARB)	(RXRB)	0.400000	0.498273
(ROR2)	(MAPK8)	0.400000	0.498273
(THRA)	(RARB)	0.400000	0.498273
(PRKCD)	(STAT1)	0.400000	0.498273
(CDK1)	(HMGA1)	0.400000	0.498273
	(MAP2K1)	0.400000	0.498273
(WWTR1)	(NKX2-1)	0.400000	0.498273
(MAP2K1)	(MAPK3)	0.400000	0.498273
(ABL1)	(CEBPB)	0.433333	0.504007
(NFKB1_RELA)	(EGR1)	0.466667	0.507416
(SMAD2)	(MEF2A)	0.466667	0.507416
(TP53)	(ETS1)	0.500000	0.508548
(MAPK3)	(ETS1)	0.500000	0.508548
(RELA)	(EGR1)	0.533333	0.507416
(MAPK14)	(MEF2A)	0.533333	0.507416
(HIPK2)	(HMGA1)	0.533333	0.507416
(JUN)	(SPI1)	0.533333	0.507416
(HIPK2)	(TP53)	0.566667	0.504007
(SMAD3)	(CEBPB)	0.566667	0.504007
(PPP2CA)	(PRKCD)	0.566667	0.504007
(THRA)	(RARG)	0.600000	0.498273
(PRKCD)	(MAPK8)	0.600000	0.498273
(RARG)	(RXRB)	0.600000	0.498273
(SMAD3)	(NKX2-1)	0.600000	0.498273
(CDC25A)	(MAPK3)	0.600000	0.498273
(MAPK8)	(STAT1)	0.600000	0.498273
(CDK1)	(CDC25A)	0.600000	0.498273
(MAPK14)	(GSK3B)	0.633333	0.490133
	(CDKN1A)	0.633333	0.490133
(MAPK1)	(APC_AXIN1_GSK3B)	0.666667	0.479463
(CSNK1D)	(WWTR1)	0.666667	0.479463
(APC_AXIN1_GSK3B)	(CSNK1D)	0.666667	0.479463
(MUC1)	(KLF4)	0.666667	0.479463
(GSK3B)	(MUC1)	0.666667	0.479463
(CDK1)	(PML)	0.666667	0.479463
(TBK1)	(IRF3)	0.666667	0.479463
(MAPK14)	(SMAD3)	0.700000	0.466092
(SMAD3)	(SMAD4)	0.700000	0.466092
(ABL1)	(RB1)	0.700000	0.466092
(PHLPP1)	(PRKCA)	0.733333	0.449776

# Analyze edge values across solutions
df_edge_val = pd.DataFrame(
    np.concatenate(edge_results["edge_values"], axis=1), index=m.processed_graph.E
).astype(int)
df_edge_val.head()

		0	1	2	3	4	5	6	7	8	9	...	20	21	22	23	24	25	26	27	28	29
(SMAD3)	(MYOD1)	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
(GRK2)	(BDKRB2)	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
(MAPK14)	(MAPKAPK2)	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
(DEPTOR_EEF1A1_MLST8_MTOR_PRR5_RICTOR)	(FBXW8)	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
(SLK)	(MAP3K5)	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0

5 rows × 30 columns

Vertex-Based Perturbation

Next, we’ll sample solutions by perturbing vertex variables. This approach can highlight alternative active node sets that are consistent with the data.

# Create a fresh model
m = CarnivalFlow(lambda_reg=0.1)
P = m.build(dataset.graph, dataset.data)

# Sample solutions by perturbing vertex_value
vertex_results = sample_alternative_solutions(
    problem=P,
    target_variable=P.expr.vertex_value,
    percentage=0.10,
    scale=0.03,
    rel_opt_tol=0.05,
    max_samples=30,
)

# Analyze vertex-based results
df_vertex_val = pd.DataFrame(
    np.concatenate(vertex_results["vertex_values"], axis=1), index=m.processed_graph.V
).astype(int)
print(f"Generated {df_vertex_val.shape[1]} alternative solutions")
df_vertex_val.head()

Unreachable vertices for sample: 0
===============================================================================
                                     CVXPY                                     
                                     v1.6.4                                    
===============================================================================
(CVXPY) Apr 10 07:11:09 PM: Your problem has 11092 variables, 31652 constraints, and 1 parameters.
(CVXPY) Apr 10 07:11:09 PM: It is compliant with the following grammars: DCP, DQCP
(CVXPY) Apr 10 07:11:09 PM: CVXPY will first compile your problem; then, it will invoke a numerical solver to obtain a solution.
(CVXPY) Apr 10 07:11:09 PM: Your problem is compiled with the CPP canonicalization backend.
-------------------------------------------------------------------------------
                                  Compilation                                  
-------------------------------------------------------------------------------
(CVXPY) Apr 10 07:11:09 PM: Compiling problem (target solver=GUROBI).
(CVXPY) Apr 10 07:11:09 PM: Reduction chain: CvxAttr2Constr -> Qp2SymbolicQp -> QpMatrixStuffing -> GUROBI
(CVXPY) Apr 10 07:11:09 PM: Applying reduction CvxAttr2Constr
(CVXPY) Apr 10 07:11:09 PM: Applying reduction Qp2SymbolicQp
(CVXPY) Apr 10 07:11:09 PM: Applying reduction QpMatrixStuffing
(CVXPY) Apr 10 07:11:09 PM: Applying reduction GUROBI
(CVXPY) Apr 10 07:11:09 PM: Finished problem compilation (took 5.829e-02 seconds).
(CVXPY) Apr 10 07:11:09 PM: (Subsequent compilations of this problem, using the same arguments, should take less time.)
-------------------------------------------------------------------------------
                                Numerical solver                               
-------------------------------------------------------------------------------
(CVXPY) Apr 10 07:11:09 PM: Invoking solver GUROBI  to obtain a solution.
Set parameter OutputFlag to value 1
Set parameter QCPDual to value 1
Gurobi Optimizer version 12.0.1 build v12.0.1rc0 (mac64[arm] - Darwin 24.4.0 24E248)

CPU model: Apple M4 Pro
Thread count: 12 physical cores, 12 logical processors, using up to 12 threads

Non-default parameters:
QCPDual  1

Optimize a model with 31652 rows, 11092 columns and 111482 nonzeros
Model fingerprint: 0x926525f9
Variable types: 4344 continuous, 6748 integer (6748 binary)
Coefficient statistics:
  Matrix range     [1e+00, 1e+03]
  Objective range  [1e-01, 8e+00]
  Bounds range     [1e+00, 1e+00]
  RHS range        [1e+00, 1e+03]
Found heuristic solution: objective 0.0000000
Presolve removed 18549 rows and 1627 columns
Presolve time: 0.15s
Presolved: 13103 rows, 9465 columns, 82774 nonzeros
Variable types: 3602 continuous, 5863 integer (5853 binary)

Root relaxation: objective -2.060081e+02, 1119 iterations, 0.02 seconds (0.05 work units)

    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

     0     0 -206.00811    0   64    0.00000 -206.00811      -     -    0s
     0     0 -202.60774    0   66    0.00000 -202.60774      -     -    0s
H    0     0                    -121.0727864 -202.45357  67.2%     -    0s
H    0     0                    -125.9042639 -202.45357  60.8%     -    0s
     0     0 -202.32031    0   64 -125.90426 -202.32031  60.7%     -    0s
     0     0 -202.27031    0   65 -125.90426 -202.27031  60.7%     -    0s
     0     0 -202.27031    0   54 -125.90426 -202.27031  60.7%     -    0s
     0     0 -202.27031    0   52 -125.90426 -202.27031  60.7%     -    0s
H    0     0                    -131.7216934 -202.27031  53.6%     -    0s
     0     0 -202.27031    0   56 -131.72169 -202.27031  53.6%     -    0s
     0     0 -202.27031    0   42 -131.72169 -202.27031  53.6%     -    0s
     0     0 -202.27031    0   40 -131.72169 -202.27031  53.6%     -    0s
H    0     0                    -134.7525108 -202.27031  50.1%     -    0s
     0     0 -202.25020    0   28 -134.75251 -202.25020  50.1%     -    0s
H    0     0                    -140.2462506 -202.22020  44.2%     -    0s
     0     0 -202.22020    0   28 -140.24625 -202.22020  44.2%     -    0s
     0     0 -202.22020    0   18 -140.24625 -202.22020  44.2%     -    0s
H    0     0                    -199.6703069 -202.20354  1.27%     -    0s
H    0     0                    -200.1703069 -202.20354  1.02%     -    0s
     0     0 -202.20354    0   18 -200.17031 -202.20354  1.02%     -    0s
H    0     0                    -201.9703069 -202.13697  0.08%     -    0s
     0     0 -202.13697    0   22 -201.97031 -202.13697  0.08%     -    0s
     0     0 -202.13697    0   22 -201.97031 -202.13697  0.08%     -    0s
     0     0 -202.07031    0    2 -201.97031 -202.07031  0.05%     -    0s
     0     0 -202.07031    0    2 -201.97031 -202.07031  0.05%     -    0s
     0     0 -202.07031    0    2 -201.97031 -202.07031  0.05%     -    0s
     0     0 -202.07031    0    5 -201.97031 -202.07031  0.05%     -    0s
     0     0 -202.07031    0    5 -201.97031 -202.07031  0.05%     -    0s
     0     0 -202.07031    0   25 -201.97031 -202.07031  0.05%     -    0s
     0     0 -202.07031    0   29 -201.97031 -202.07031  0.05%     -    0s
     0     0 -202.07031    0   29 -201.97031 -202.07031  0.05%     -    0s
     0     0 -202.07031    0   22 -201.97031 -202.07031  0.05%     -    0s
     0     0 -202.07031    0   26 -201.97031 -202.07031  0.05%     -    0s
     0     0 -202.07031    0   26 -201.97031 -202.07031  0.05%     -    0s
     0     0 -202.07031    0   23 -201.97031 -202.07031  0.05%     -    0s
     0     0 -202.07031    0   26 -201.97031 -202.07031  0.05%     -    0s
     0     0 -202.07031    0    6 -201.97031 -202.07031  0.05%     -    0s

Cutting planes:
  Learned: 2
  Gomory: 4
  Cover: 1
  Implied bound: 11
  Clique: 4
  MIR: 9
  Zero half: 7
  Mod-K: 1
  RLT: 10
  Relax-and-lift: 1
  BQP: 1
  PSD: 2

Explored 1 nodes (4497 simplex iterations) in 0.86 seconds (1.20 work units)
Thread count was 12 (of 12 available processors)

Solution count 9: -201.97 -200.17 -199.67 ... 0
No other solutions better than -201.97

Optimal solution found (tolerance 1.00e-04)
Best objective -2.019703069210e+02, best bound -2.019703069210e+02, gap 0.0000%
-------------------------------------------------------------------------------
                                    Summary                                    
-------------------------------------------------------------------------------
(CVXPY) Apr 10 07:11:10 PM: Problem status: optimal
(CVXPY) Apr 10 07:11:10 PM: Optimal value: 1.622e+01
(CVXPY) Apr 10 07:11:10 PM: Compilation took 5.829e-02 seconds
(CVXPY) Apr 10 07:11:10 PM: Solver (including time spent in interface) took 8.972e-01 seconds
error_sample1_0 7.0169713497161865
multi_sample_regularization_edge_has_signal 92.0
Sample 1/30: Objective value = 16.2117
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 2/30: Objective value = 16.2916
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 93.0000, rel error: 0.0109
Sample 3/30: Objective value = 16.2261
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 4/30: Objective value = 16.2643
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 5/30: Objective value = 16.3308
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 6/30: Objective value = 16.2693
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 7/30: Objective value = 16.3319
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 8/30: Objective value = 16.1480
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 9/30: Objective value = 16.3680
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 10/30: Objective value = 16.1878
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 11/30: Objective value = 16.0145
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 12/30: Objective value = 16.0929
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 13/30: Objective value = 16.3187
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 14/30: Objective value = 16.1250
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 15/30: Objective value = 16.1789
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 16/30: Objective value = 16.2809
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 17/30: Objective value = 16.3439
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 18/30: Objective value = 16.1387
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 19/30: Objective value = 16.1296
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 20/30: Objective value = 16.1100
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 21/30: Objective value = 16.2697
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 22/30: Objective value = 16.1848
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 23/30: Objective value = 16.0936
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 24/30: Objective value = 16.1869
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 25/30: Objective value = 16.2711
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 26/30: Objective value = 16.1187
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 27/30: Objective value = 16.2951
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 28/30: Objective value = 16.2525
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 29/30: Objective value = 16.2769
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Sample 30/30: Objective value = 16.1914
  error_sample1_0: 7.0170, rel error: 0.0000
  multi_sample_regularization_edge_has_signal: 92.0000, rel error: 0.0000
Generated 30 alternative solutions

	0	1	2	3	4	5	6	7	8	9	...	20	21	22	23	24	25	26	27	28	29
DIAPH1	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
PRKD1	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
ALDH2	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
MDM2	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
RAD21	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0

5 rows × 30 columns

# Focus on signaling proteins with no measurement data
df_sig_prot_pred = df_vertex_val.loc[
    df_vertex_val.index.difference(dataset.data.query.pluck_features())
]
df_sig_prot_pred.head()

	0	1	2	3	4	5	6	7	8	9	...	20	21	22	23	24	25	26	27	28	29
AAK1	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
ABI1	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
ABL1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	...	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1
ABL2	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
ABRAXAS1	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0

5 rows × 30 columns

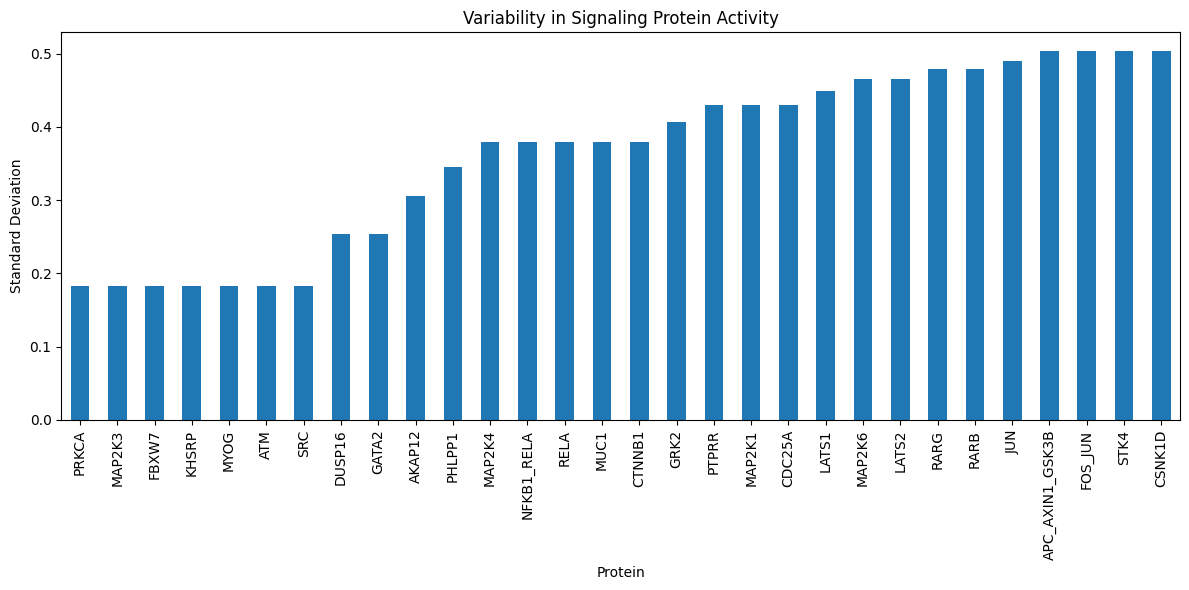
# Visualize the variability in predicted signaling protein activities
import matplotlib.pyplot as plt

plt.figure(figsize=(12, 6))
df_sig_prot_pred.std(axis=1).sort_values().tail(30).plot.bar(
    title="Variability in Signaling Protein Activity"
)
plt.xlabel("Protein")
plt.ylabel("Standard Deviation")
plt.tight_layout()
plt.show()

Summary

In this notebook, we:

1. Created a generic sampling method for exploring alternative network solutions

2. Applied the method to both edge and vertex perturbations

3. Analyzed the variability in solutions to identify:

   • Edges with high uncertainty (appearing in some but not all solutions)

   • Signaling proteins with variable activity across solutions

This approach helps assess the robustness of network inference results and can guide further experimental validation efforts by highlighting the most uncertain parts of the network.