Flux Balance Analysis (FBA)#
Flux Balance Analysis (FBA) is a computational method used primarily in systems biology and metabolic engineering. It’s a way to understand and predict the flow or “flux” of metabolites in a metabolic network under certain conditions.
In this tutorial, we will see how to create FBA problems with CORNETO for metabolic analysis, how CORNETO can interoperate with other FBA-based libraries such as COBRApy or MIOM, and how CORNETO’s FBA problem can be used as a building block for more advanced FBA methods.
What is FBA?#
The basis of FBA lies in the principle of steady-state, where the concentration of internal metabolites doesn’t change over time even though they may be consumed and produced. This means that the total rate at which a metabolite is produced equals the rate at which it’s consumed.
In the realm of metabolic network analysis, this concept translates to steady-state metabolic fluxes. A flux is a rate at which a substance moves through a system, and in metabolic systems, flux represents the rate of turnover of a metabolite through a specific pathway or reaction. When considering the steady-state, each reaction’s flux in the metabolic network is balanced, meaning that, for every internal metabolite, the sum of fluxes leading to its production is equal to the sum of fluxes leading to its consumption. This balance ensures that, over time, there’s no accumulation or depletion of any metabolite in the system.
For quantifying these fluxes, the typical units used are millimoles per gram dry weight per hour (mmol/gDW/h). The “mmol” part represents the quantity of the metabolite, the “gDW” (gram dry weight) normalizes this value to the biomass of the organism, and the “/h” provides a temporal dimension, indicating how fast the metabolic turnover occurs. This unit allows researchers and practitioners to make meaningful comparisons across different metabolic systems and conditions. For example, a flux value of 5 mmol/gDW/h for a particular reaction indicates that 5 millimoles of the relevant metabolite are produced or consumed per gram of the organism’s dry weight every hour.
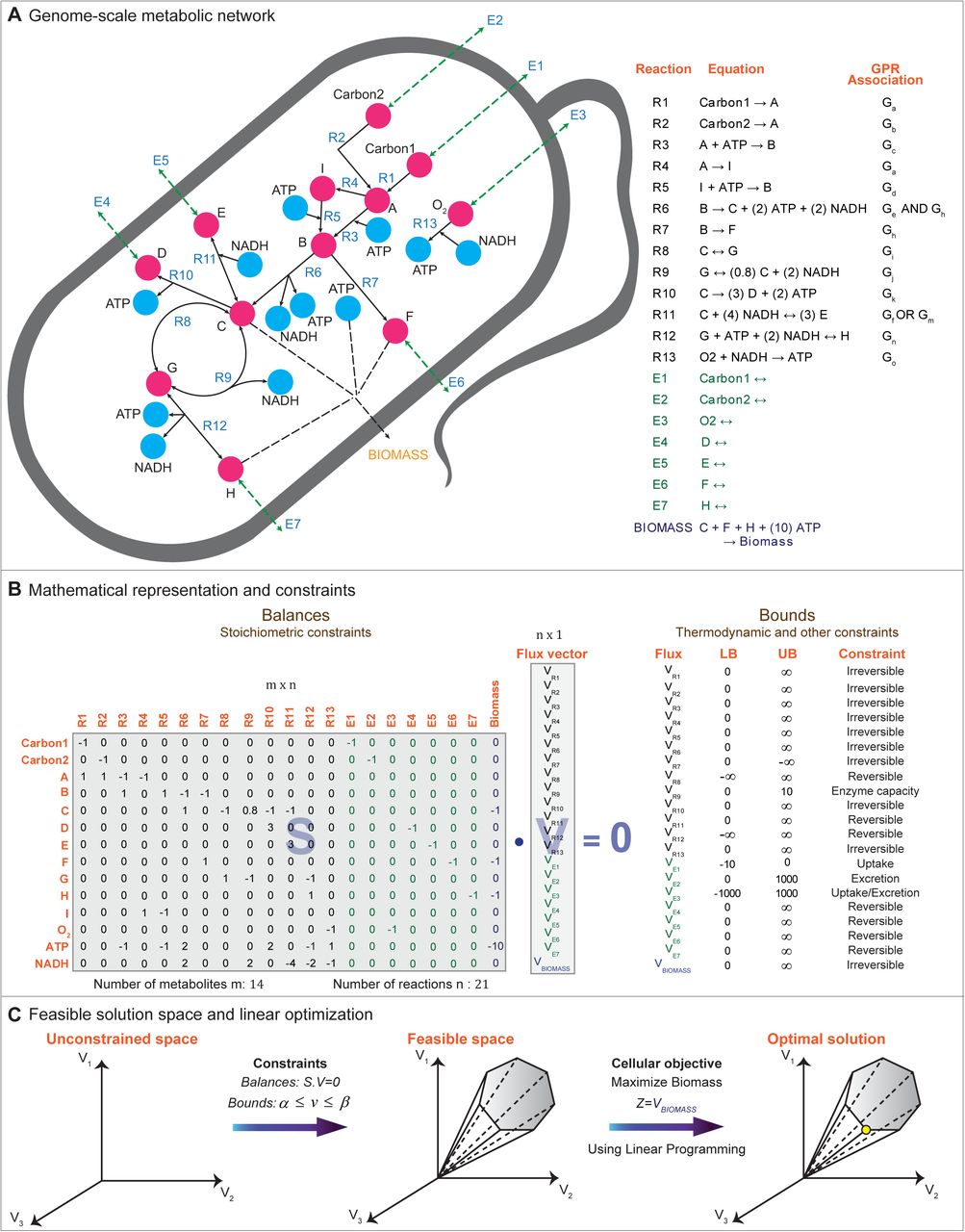
Figure 1: Vivek-Ananth, R. P., and Areejit Samal. "Advances in the integration of transcriptional regulatory information into genome-scale metabolic models." Biosystems 147 (2016): 1-10.
FBA with CORNETO#
In order to define a FBA problem, you need to know the following:
Genome-scale metabolic network: This is the prior knowledge, usually known as genome-scale metabolic models (GEMs). These models represent the metabolic network through a stoichiometric matrix, where each row represents a metabolite and each column represents a reaction. The entries in the matrix are the stoichiometric coefficients of the metabolites in the reactions. These models also contain annotations such as Gene-Protein-Rules (GPRs) and default reaction bounds.
Constraints: For each reaction, there are limits or “constraints” on the flux based on factors like enzyme capacities. Basically, it’s setting the maximum and minimum fluxes for the reactions.
Objective function: You then define an objective to optimize, like maximizing the production of a specific metabolite or maximizing growth rate.
LP Solver: Using linear programming techniques, you can find the flux distribution that meets the constraints and optimizes the objective function.
CORNETO naturally supports FBA-based problems by transforming a genome scale metabolic network into a prior knowledge graph, and then modelling the FBA problem as a network flow problem. This is the main building block for creating more complex problems, such as multicondition Sparse FBA or multicondition iMAT for context-specific reconstruction.
Using COBRApy#
Here we show how can we use COBRApy to import the textbook metabolic network and how can we import it in CORNETO. We will also compare the FBA solution from COBRApy and CORNETO.
from cobra.io import load_model
model = load_model("textbook")
len(model.metabolites), len(model.reactions)
(72, 95)
biomass_rxn = model.reactions.get_by_id("Biomass_Ecoli_core")
biomass_rxn
| Reaction identifier | Biomass_Ecoli_core |
| Name | Biomass Objective Function with GAM |
| Memory address | 0x7f696cc2d590 |
| Stoichiometry |
1.496 3pg_c + 3.7478 accoa_c + 59.81 atp_c + 0.361 e4p_c + 0.0709 f6p_c + 0.129 g3p_c + 0.205 g6p_c + 0.2557 gln__L_c + 4.9414 glu__L_c + 59.81 h2o_c + 3.547 nad_c + 13.0279 nadph_c + 1.7867 oaa_c... 1.496 3-Phospho-D-glycerate + 3.7478 Acetyl-CoA + 59.81 ATP + 0.361 D-Erythrose 4-phosphate + 0.0709 D-Fructose 6-phosphate + 0.129 Glyceraldehyde 3-phosphate + 0.205 D-Glucose 6-phosphate + 0.2557... |
| GPR | |
| Lower bound | 0.0 |
| Upper bound | 1000.0 |
solution = model.optimize()
print(solution)
<Solution 0.874 at 0x7f696cc5fc50>
Using CORNETO#
import corneto as cn
import numpy as np
cn.info()
|
|
from corneto.io import cobra_model_to_graph
G = cobra_model_to_graph(model)
G.shape
(72, 95)
rid = list(G.get_edges_by_attr("id", biomass_rxn.id))[0]
G.get_attr_edge(rid)
{'__edge_type': 'directed',
'id': 'Biomass_Ecoli_core',
'__source_attr': {'3pg_c': {'__value': np.float64(-1.496)},
'accoa_c': {'__value': np.float64(-3.7478)},
'atp_c': {'__value': np.float64(-59.81)},
'e4p_c': {'__value': np.float64(-0.361)},
'f6p_c': {'__value': np.float64(-0.0709)},
'g3p_c': {'__value': np.float64(-0.129)},
'g6p_c': {'__value': np.float64(-0.205)},
'gln__L_c': {'__value': np.float64(-0.2557)},
'glu__L_c': {'__value': np.float64(-4.9414)},
'h2o_c': {'__value': np.float64(-59.81)},
'nad_c': {'__value': np.float64(-3.547)},
'nadph_c': {'__value': np.float64(-13.0279)},
'oaa_c': {'__value': np.float64(-1.7867)},
'pep_c': {'__value': np.float64(-0.5191)},
'pyr_c': {'__value': np.float64(-2.8328)},
'r5p_c': {'__value': np.float64(-0.8977)}},
'__target_attr': {'adp_c': {'__value': np.float64(59.81)},
'akg_c': {'__value': np.float64(4.1182)},
'coa_c': {'__value': np.float64(3.7478)},
'h_c': {'__value': np.float64(59.81)},
'nadh_c': {'__value': np.float64(3.547)},
'nadp_c': {'__value': np.float64(13.0279)},
'pi_c': {'__value': np.float64(59.81)}},
'default_lb': np.float64(0.0),
'default_ub': np.float64(1000.0),
'GPR': ''}
G.plot(layout="fdp")
from corneto.methods.future import MultiSampleFBA as FBA
d = cn.Data.from_cdict(
{
"fba_example": {
"Biomass_Ecoli_core": {
"role": "objective"
}
}
}
)
m = FBA()
P = m.build(G, d)
P.expr
{'_flow': _flow: Variable((95,), _flow),
'edge_has_flux': edge_has_flux: Variable((95,), edge_has_flux, boolean=True),
'flow': _flow: Variable((95,), _flow)}
P.solve(solver="scipy");
opt_flux = P.expr.flow[rid].value
opt_flux
np.float64(0.873921506968431)
sum(np.abs(P.expr.flow.value) >= 1e-6)
np.int64(48)
import pandas as pd
pd.DataFrame(P.expr.flow.value, index=G.get_attr_from_edges("id"), columns=["fluxes"])
| fluxes | |
|---|---|
| ACALD | -0.000000 |
| ACALDt | 0.000000 |
| ACKr | 0.000000 |
| ACONTa | 6.007250 |
| ACONTb | 6.007250 |
| ... | ... |
| TALA | 1.496984 |
| THD2 | 0.000000 |
| TKT1 | 1.496984 |
| TKT2 | 1.181498 |
| TPI | 7.477382 |
95 rows × 1 columns
G.plot(custom_edge_attr=cn.pl.flow_style(P), layout="fdp")
Sparse FBA#
m = FBA(lambda_reg=0.1)
P = m.build(G, d)
# We add a constraint to force at least 90% of optimal flux
P += P.expr.flow[rid] >= opt_flux*0.90
P.solve(solver="highs", verbosity=1);
===============================================================================
CVXPY
v1.6.5
===============================================================================
(CVXPY) Apr 17 03:25:19 PM: Your problem has 190 variables, 453 constraints, and 1 parameters.
(CVXPY) Apr 17 03:25:19 PM: It is compliant with the following grammars: DCP, DQCP
(CVXPY) Apr 17 03:25:19 PM: CVXPY will first compile your problem; then, it will invoke a numerical solver to obtain a solution.
(CVXPY) Apr 17 03:25:19 PM: Your problem is compiled with the CPP canonicalization backend.
-------------------------------------------------------------------------------
Compilation
-------------------------------------------------------------------------------
(CVXPY) Apr 17 03:25:19 PM: Compiling problem (target solver=HIGHS).
(CVXPY) Apr 17 03:25:19 PM: Reduction chain: Dcp2Cone -> CvxAttr2Constr -> ConeMatrixStuffing -> HIGHS
(CVXPY) Apr 17 03:25:19 PM: Applying reduction Dcp2Cone
(CVXPY) Apr 17 03:25:19 PM: Applying reduction CvxAttr2Constr
(CVXPY) Apr 17 03:25:19 PM: Applying reduction ConeMatrixStuffing
(CVXPY) Apr 17 03:25:19 PM: Applying reduction HIGHS
(CVXPY) Apr 17 03:25:19 PM: Finished problem compilation (took 1.042e-02 seconds).
(CVXPY) Apr 17 03:25:19 PM: (Subsequent compilations of this problem, using the same arguments, should take less time.)
-------------------------------------------------------------------------------
Numerical solver
-------------------------------------------------------------------------------
(CVXPY) Apr 17 03:25:19 PM: Invoking solver HIGHS to obtain a solution.
Running HiGHS 1.10.0 (git hash: fd86653): Copyright (c) 2025 HiGHS under MIT licence terms
MIP has 453 rows; 190 cols; 883 nonzeros; 95 integer variables (95 binary)
Coefficient ranges:
Matrix [7e-02, 1e+03]
Cost [1e-01, 1e+00]
Bound [1e+00, 1e+00]
RHS [8e-01, 1e+03]
Presolving model
153 rows, 144 cols, 493 nonzeros 0s
123 rows, 123 cols, 415 nonzeros 0s
120 rows, 119 cols, 408 nonzeros 0s
Solving MIP model with:
120 rows
119 cols (78 binary, 0 integer, 0 implied int., 41 continuous)
408 nonzeros
Src: B => Branching; C => Central rounding; F => Feasibility pump; H => Heuristic; L => Sub-MIP;
P => Empty MIP; R => Randomized rounding; S => Solve LP; T => Evaluate node; U => Unbounded;
z => Trivial zero; l => Trivial lower; u => Trivial upper; p => Trivial point; X => User solution
Nodes | B&B Tree | Objective Bounds | Dynamic Constraints | Work
Src Proc. InQueue | Leaves Expl. | BestBound BestSol Gap | Cuts InLp Confl. | LpIters Time
0 0 0 0.00% -64.93809816 inf inf 0 0 0 0 0.0s
S 0 0 0 0.00% -64.93809816 3.685702492 1861.89% 0 0 0 0 0.0s
0 0 0 0.00% 0.5684850774 3.685702492 84.58% 0 0 0 55 0.0s
7.7% inactive integer columns, restarting
Model after restart has 109 rows, 113 cols (72 bin., 0 int., 0 impl., 41 cont.), and 382 nonzeros
0 0 0 0.00% 2.159371619 3.685702492 41.41% 35 0 0 2185 0.3s
0 0 0 0.00% 2.159371619 3.685702492 41.41% 35 34 0 2241 0.3s
Symmetry detection completed in 0.0s
Found 17 full orbitope(s) acting on 40 columns
97 0 49 100.00% 3.685702492 3.685702492 0.00% 1849 32 649 7352 0.9s
Solving report
Status Optimal
Primal bound 3.68570249247
Dual bound 3.68570249247
Gap 0% (tolerance: 0.01%)
P-D integral 0.302663181423
Solution status feasible
3.68570249247 (objective)
0 (bound viol.)
0 (int. viol.)
0 (row viol.)
Timing 0.86 (total)
0.00 (presolve)
0.00 (solve)
0.00 (postsolve)
Max sub-MIP depth 3
Nodes 97
Repair LPs 0 (0 feasible; 0 iterations)
LP iterations 7352 (total)
2147 (strong br.)
868 (separation)
3383 (heuristics)
-------------------------------------------------------------------------------
Summary
-------------------------------------------------------------------------------
(CVXPY) Apr 17 03:25:20 PM: Problem status: optimal
(CVXPY) Apr 17 03:25:20 PM: Optimal value: 3.686e+00
(CVXPY) Apr 17 03:25:20 PM: Compilation took 1.042e-02 seconds
(CVXPY) Apr 17 03:25:20 PM: Solver (including time spent in interface) took 8.644e-01 seconds
G.plot(custom_edge_attr=cn.pl.flow_style(P), layout="fdp")
sum(P.expr.edge_has_flux.value > 0.5)
np.int64(45)
P.objectives
[objective_Biomass_Ecoli_core: Expression(AFFINE, UNKNOWN, ()),
regularization_edge_has_flux: Expression(AFFINE, NONNEGATIVE, ())]
P.objectives[1].value
np.float64(45.0)