Multi-sample PCST#
Here we demonstrate the use of the multi-sample PCST method, and we also compare against the standard single sample PCST approximation implemented in the pcst_fast package
import networkx as nx
import random
import numpy as np
import pcst_fast # Ensure pcst_fast is installed
import matplotlib.pyplot as plt
def generate_random_graph(num_nodes=100, probability=0.1, num_terminals=10):
"""
Generates a random unweighted graph using the Erdős-Rényi model and assigns terminal nodes.
Prizes are not assigned during generation.
Args:
num_nodes (int): Number of nodes in the graph.
probability (float): Probability for edge creation.
num_terminals (int): Number of nodes to mark as terminals.
Returns:
G (networkx.Graph): Graph with a 'terminal' attribute on nodes.
"""
G = nx.erdos_renyi_graph(num_nodes, probability)
# Randomly select terminal nodes
terminals = random.sample(list(G.nodes()), min(num_terminals, G.number_of_nodes()))
for node in G.nodes():
G.nodes[node]['terminal'] = (node in terminals)
return G
def assign_random_costs_and_prizes(G, num_prized=10, prize_range=(1, 50)):
"""
Creates a new copy of the given graph, assigns random edge costs and prizes.
The original graph remains unchanged. Edge costs are stored in the 'value' attribute.
Only a specified number of non-terminal nodes receive a random prize; all other nodes are assigned a prize of 0.
Args:
G (networkx.Graph): The input graph whose topology is preserved.
num_prized (int): The number of non-terminal nodes to receive a prize.
prize_range (tuple): Tuple (min, max) for random prize values.
Returns:
G_new (networkx.Graph): A new graph with updated 'value' attributes on edges and 'prize' attributes on nodes.
"""
# Create a copy of the graph so the original is not modified.
G_new = G.copy()
# Assign random edge costs
for u, v in G_new.edges():
G_new[u][v]['value'] = random.uniform(1, 10)
# Identify non-terminal nodes
non_terminal_nodes = [node for node in G_new.nodes() if not G_new.nodes[node].get('terminal', False)]
# Randomly select nodes to assign prizes (do not exceed available nodes)
prized_nodes = random.sample(non_terminal_nodes, min(num_prized, len(non_terminal_nodes)))
# Assign prizes: nodes selected get a random prize, all others get 0
for node in G_new.nodes():
if node in prized_nodes:
G_new.nodes[node]['prize'] = random.uniform(*prize_range)
else:
G_new.nodes[node]['prize'] = 0
return G_new
def solve_pcst_with_pcst_fast(G, root=-1, num_clusters=1, pruning='strong', verbosity=0):
"""
Solves the PCST problem on a NetworkX graph using the pcst_fast package.
Args:
G (networkx.Graph): Graph with 'value' on edges and 'prize' on nodes.
root (int): Index of the root node (or -1 for unrooted).
num_clusters (int): Desired number of clusters in the solution.
pruning (str): Pruning method ('none', 'simple', 'gw', 'strong').
verbosity (int): Verbosity level.
Returns:
selected_nodes (list): Node IDs included in the PCST solution.
selected_edges (list): Edge tuples included in the solution.
"""
node_list = list(G.nodes())
node_index_map = {node: i for i, node in enumerate(node_list)}
index_node_map = {i: node for node, i in node_index_map.items()}
edge_list = []
edge_costs = []
for u, v, data in G.edges(data=True):
edge_list.append([node_index_map[u], node_index_map[v]])
edge_costs.append(data['value'])
prizes = np.array([G.nodes[node].get('prize', 0) for node in node_list], dtype=np.float64)
edges_array = np.array(edge_list, dtype=np.int64)
costs_array = np.array(edge_costs, dtype=np.float64)
vertices_out, edges_out = pcst_fast.pcst_fast(
edges_array,
prizes,
costs_array,
root,
num_clusters,
pruning,
verbosity
)
selected_nodes = [index_node_map[i] for i in vertices_out]
selected_edges = [tuple(node_list[idx] for idx in edge_list[i]) for i in edges_out]
return selected_nodes, selected_edges
def compute_pcst_cost(G, selected_edges):
"""
Calculates the cost components and total PCST objective value based solely on the selected edges.
The function:
- Derives the set of selected nodes from the provided edges.
- Builds a graph using only the selected edges.
- Checks that the selected edges form a single connected subgraph.
Returns:
dict with keys 'edge_cost', 'prize_collected', and 'objective'
Raises:
ValueError: If any provided edge is not in G or if the selected edges do not form a connected subgraph.
"""
# Derive selected nodes from edges and verify edge validity
selected_nodes = set()
for u, v in selected_edges:
if not G.has_edge(u, v):
raise ValueError(f"Edge ({u}, {v}) is not present in the graph.")
selected_nodes.update([u, v])
# For non-empty selections, check connectivity using only the selected edges.
if selected_edges:
H = nx.Graph()
H.add_nodes_from(selected_nodes)
H.add_edges_from(selected_edges)
if not nx.is_connected(H):
raise ValueError("Selected edges do not form a connected subgraph.")
# Calculate the total edge cost.
edge_cost = sum(G[u][v]['value'] for u, v in selected_edges)
# Sum the prizes for all nodes in the connected subgraph.
prize_collected = sum(G.nodes[n].get('prize', 0) for n in selected_nodes)
objective = edge_cost - prize_collected
return {
'edge_cost': edge_cost,
'prize_collected': prize_collected,
'objective': objective
}
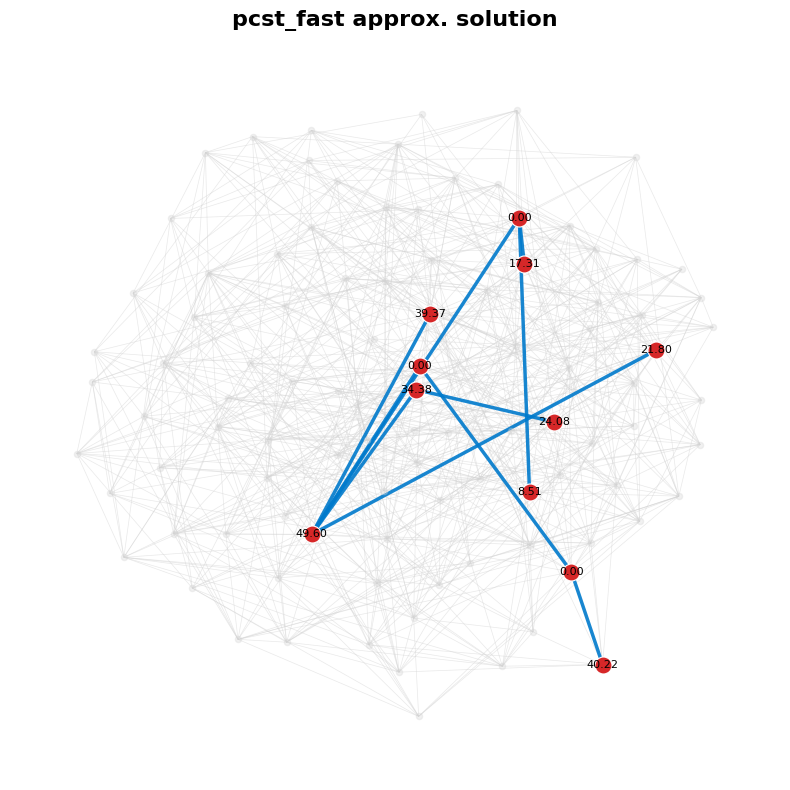
def visualize(G, selected_nodes, selected_edges):
pos = nx.forceatlas2_layout(G, dissuade_hubs=False, seed=42)
plt.figure(figsize=(8, 8))
# Base layer: faint background graph
nx.draw_networkx_edges(G, pos, alpha=0.5, width=0.5, edge_color='lightgray')
nx.draw_networkx_nodes(G, pos, node_size=20, node_color='lightgray', alpha=0.3)
# Selected edges (solution)
nx.draw_networkx_edges(G, pos, edgelist=selected_edges, width=2.5, edge_color='#007acc', alpha=0.9)
# Selected nodes (solution)
nx.draw_networkx_nodes(G, pos, nodelist=selected_nodes, node_size=150, node_color='#d62728', edgecolors='white', linewidths=0.8)
# Optional: add labels or prizes
node_labels = {n: f"{(G.nodes[n].get('prize', 0)):.2f}" for n in selected_nodes}
nx.draw_networkx_labels(G, pos, labels=node_labels, font_size=8, font_color='black')
plt.title("pcst_fast approx. solution", fontsize=16, fontweight='bold', pad=15)
plt.axis('off')
plt.tight_layout()
plt.show()
random.seed(10)
# 1. Generate the base graph with a fixed topology (no prizes assigned).
G_original = generate_random_graph(num_nodes=100, probability=0.15, num_terminals=5)
# 2. Create two different samples
G_0 = assign_random_costs_and_prizes(G_original, num_prized=8, prize_range=(1, 50))
G_1 = assign_random_costs_and_prizes(G_original, num_prized=12, prize_range=(1, 50))
# 3. Get an heuristic solution with pcst_fast
selected_nodes_0, selected_edges_0 = solve_pcst_with_pcst_fast(G_0)
selected_nodes_1, selected_edges_1 = solve_pcst_with_pcst_fast(G_1)
compute_pcst_cost(G_0, selected_edges_0), compute_pcst_cost(G_1, selected_edges_1)
({'edge_cost': 25.822958394858087,
'prize_collected': 235.26839405807772,
'objective': -209.44543566321963},
{'edge_cost': 34.323495165255245,
'prize_collected': 310.25687273661805,
'objective': -275.9333775713628})
visualize(G_0, selected_nodes_0, selected_edges_0)
Using CORNETO#
import corneto as cn
cn.info()
|
|
|
# This notebook requires Gurobi
from corneto.utils import check_gurobi
check_gurobi()
Gurobipy successfully imported.
Gurobi environment started successfully.
Starting optimization of the test model...
Test optimization was successful.
Gurobi environment disposed.
Gurobi is correctly installed and working.
True
from corneto.contrib.networkx import networkx_to_corneto_graph, corneto_graph_to_networkx
Gc0 = networkx_to_corneto_graph(G_0)
Gc0.shape
(100, 685)
from corneto._data import Data
def get_data(G):
features = []
for i, attr in enumerate(G.get_attr_edges()):
features.append(dict(id=i, mapping="edge", value=attr.value))
for v in G.V:
attr = G.get_attr_vertex(v)
if attr['terminal'] and not attr.get('prize', None):
#features.append(dict(id=v, mapping="vertex", role="terminal"))
pass
elif attr.get('prize', None):
features.append(dict(id=v, mapping="vertex", role="prize", value=attr['prize']))
D = Data.from_dict({"s1": {"features": features}})
return D
def get_edge_list(graph):
edges = []
for s, t in graph.E:
s = list(s)
t = list(t)
if len(s) > 0:
s = list(s)[0]
else:
continue
if len(t) > 0:
t = list(t)[0]
else:
continue
edges.append((s, t))
return edges
D = get_data(Gc0)
D
Data(n_samples=1, n_feats=[693])
from corneto.methods.future.pcst import PrizeCollectingSteinerTree as PCST
m = PCST(lambda_reg=0, strict_acyclic=True)
P = m.build(Gc0, D)
P.solve(solver="gurobi", verbosity=0, TimeLimit=300);
Set parameter Username
Set parameter LicenseID to value 2593994
Academic license - for non-commercial use only - expires 2025-12-02
for o in P.objectives:
print(o.value)
25.822958394858087
235.26839405807772
18.0
P.objectives[0].value - P.objectives[1].value
-209.44543566321963
G0_sol = m.processed_graph.edge_subgraph(np.flatnonzero(P.expr.with_flow.value > 0.5))
compute_pcst_cost(G_0, get_edge_list(G0_sol))
{'edge_cost': 25.822958394858087,
'prize_collected': 235.26839405807772,
'objective': -209.44543566321963}
Gc1 = networkx_to_corneto_graph(G_1)
m = PCST(lambda_reg=0, strict_acyclic=True)
P = m.build(Gc1, get_data(Gc1))
P.solve(solver="gurobi", verbosity=0, TimeLimit=300);
G1_sol = m.processed_graph.edge_subgraph(np.flatnonzero(P.expr.with_flow.value > 0.5))
compute_pcst_cost(G_1, get_edge_list(G1_sol))
{'edge_cost': 36.85287997763584,
'prize_collected': 315.445743958666,
'objective': -278.5928639810302}
# pcst_fast sol
compute_pcst_cost(G_1, selected_edges_1)
{'edge_cost': 34.323495165255245,
'prize_collected': 310.25687273661805,
'objective': -275.9333775713628}
Multi-sample PCST#
Now we use multi-sample PCST to simultaneously solve both problems, using the structured sparsity regularization.
# Lets combine both problems into one multi PCST
dataset = get_data(Gc0)
dataset.add_sample("s2", get_data(Gc1).samples["s1"])
dataset
Data(n_samples=2, n_feats=[693 697])
Gc_original = networkx_to_corneto_graph(G_original)
m = PCST(lambda_reg=0, strict_acyclic=True, root_selection_strategy="best")
P = m.build(Gc_original, dataset)
P.solve(solver="gurobi", verbosity=0, TimeLimit=30);
# With no regularization, solutions should be the same
G0_sol = m.processed_graph.edge_subgraph(np.flatnonzero(P.expr.with_flow.value[:,0] > 0.5))
compute_pcst_cost(G_0, get_edge_list(G0_sol))
{'edge_cost': 25.822958394858087,
'prize_collected': 235.26839405807772,
'objective': -209.44543566321963}
G1_sol = m.processed_graph.edge_subgraph(np.flatnonzero(P.expr.with_flow.value[:,1] > 0.5))
compute_pcst_cost(G_1, get_edge_list(G1_sol))
{'edge_cost': 36.85287997763584,
'prize_collected': 315.445743958666,
'objective': -278.5928639810302}
m.processed_graph.edge_subgraph(np.flatnonzero(P.expr.with_flow.value[:,0]>0.5)).plot(layout="neato")
m.processed_graph.edge_subgraph(np.flatnonzero(P.expr.with_flow.value[:,1]>0.5)).plot(layout="neato")
Testing the effect of \(\lambda\)#
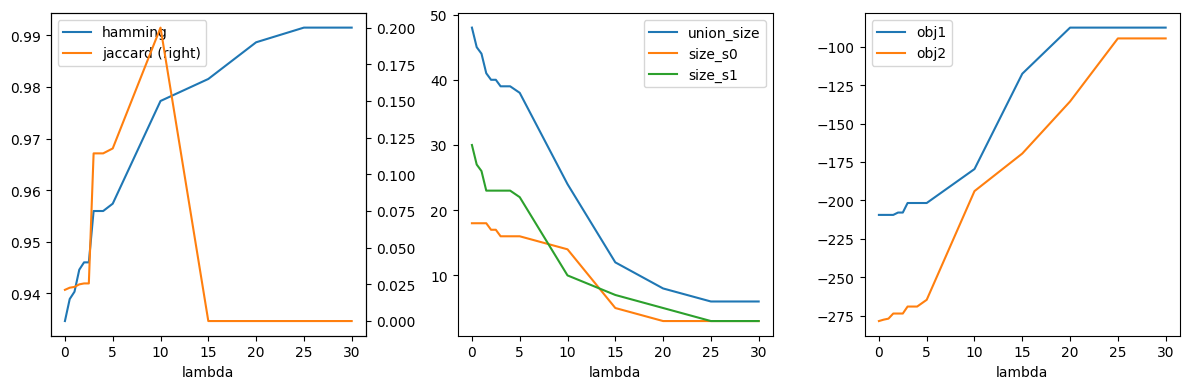
We now evaluate the impact of the structured sparsity-inducing penalty, which encourages entire sets of edges to be excluded across all samples. This penalty helps enforce group-level sparsity, effectively removing certain features from all models simultaneously. To speed up the optimization process, we also leverage Gurobi’s warm-start capability. By setting warm_start = True, we can adjust the penalty parameter \(\lambda\) and resolve the problem more efficiently, without needing to rebuild the entire optimization model from scratch.
def jaccard_similarity(a, b):
intersection = np.logical_and(a, b).sum()
union = np.logical_or(a, b).sum()
if union == 0:
return 1.0 # Define similarity as 1 if both are all zeros
return intersection / union
def hamming_similarity(a, b):
return (a == b).sum() / len(a)
results = []
for l in [0.0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 5.0, 10.0, 15.0, 20.0, 25.0, 30.0]:
print(f"Lambda = {l}")
m.lambda_reg_param.value = l
P.solve(solver="gurobi", warm_start=True, verbosity=0, TimeLimit=120);
sol0 = m.processed_graph.edge_subgraph(np.flatnonzero(P.expr.with_flow.value[:,0] > 0.5))
sol1 = m.processed_graph.edge_subgraph(np.flatnonzero(P.expr.with_flow.value[:,1] > 0.5))
# Network union size
size_0 = np.sum(P.expr.with_flow.value[:,0] > 0.5)
size_1 = np.sum(P.expr.with_flow.value[:,1] > 0.5)
union_size = np.sum(P.expr.with_flow.value > 0.5, axis=1).sum()
score1 = compute_pcst_cost(G_0, get_edge_list(sol0))
score2 = compute_pcst_cost(G_1, get_edge_list(sol1))
jaccard = jaccard_similarity(P.expr.with_flow.value[:, 0], P.expr.with_flow.value[:, 1])
hamming = hamming_similarity(P.expr.with_flow.value[:, 0], P.expr.with_flow.value[:, 1])
results.append((l, score1["objective"], score2["objective"], jaccard, hamming, union_size, size_0, size_1))
print(" > Obj. sample 1:", score1)
print(" > Obj. sample 2:", score2)
print(" > Jaccard dist.:", jaccard)
print(" > Hamming dist.:", hamming)
Lambda = 0.0
> Obj. sample 1: {'edge_cost': 25.822958394858087, 'prize_collected': 235.26839405807772, 'objective': -209.44543566321963}
> Obj. sample 2: {'edge_cost': 36.85287997763584, 'prize_collected': 315.445743958666, 'objective': -278.5928639810302}
> Jaccard dist.: 0.02127659574468085
> Hamming dist.: 0.9346590909090909
Lambda = 0.5
> Obj. sample 1: {'edge_cost': 25.822958394858087, 'prize_collected': 235.26839405807772, 'objective': -209.44543566321963}
> Obj. sample 2: {'edge_cost': 32.57672368032401, 'prize_collected': 310.25687273661805, 'objective': -277.68014905629406}
> Jaccard dist.: 0.022727272727272728
> Hamming dist.: 0.9389204545454546
Lambda = 1.0
> Obj. sample 1: {'edge_cost': 25.822958394858087, 'prize_collected': 235.26839405807772, 'objective': -209.44543566321963}
> Obj. sample 2: {'edge_cost': 33.23852158520403, 'prize_collected': 310.25687273661805, 'objective': -277.01835115141404}
> Jaccard dist.: 0.023255813953488372
> Hamming dist.: 0.9403409090909091
Lambda = 1.5
> Obj. sample 1: {'edge_cost': 25.822958394858087, 'prize_collected': 235.26839405807772, 'objective': -209.44543566321963}
> Obj. sample 2: {'edge_cost': 32.675953291132046, 'prize_collected': 306.3730702170471, 'objective': -273.69711692591505}
> Jaccard dist.: 0.025
> Hamming dist.: 0.9446022727272727
Lambda = 2.0
> Obj. sample 1: {'edge_cost': 27.354768134907065, 'prize_collected': 235.26839405807772, 'objective': -207.91362592317066}
> Obj. sample 2: {'edge_cost': 32.675953291132046, 'prize_collected': 306.3730702170471, 'objective': -273.69711692591505}
> Jaccard dist.: 0.02564102564102564
> Hamming dist.: 0.9460227272727273
Lambda = 2.5
> Obj. sample 1: {'edge_cost': 27.354768134907065, 'prize_collected': 235.26839405807772, 'objective': -207.91362592317066}
> Obj. sample 2: {'edge_cost': 32.675953291132046, 'prize_collected': 306.3730702170471, 'objective': -273.69711692591505}
> Jaccard dist.: 0.02564102564102564
> Hamming dist.: 0.9460227272727273
Lambda = 3.0
> Obj. sample 1: {'edge_cost': 25.06505287957105, 'prize_collected': 226.7623826795313, 'objective': -201.69732979996024}
> Obj. sample 2: {'edge_cost': 37.23012326447901, 'prize_collected': 306.3730702170471, 'objective': -269.1429469525681}
> Jaccard dist.: 0.11428571428571428
> Hamming dist.: 0.9559659090909091
Lambda = 3.5
> Obj. sample 1: {'edge_cost': 25.06505287957105, 'prize_collected': 226.7623826795313, 'objective': -201.69732979996024}
> Obj. sample 2: {'edge_cost': 37.23012326447901, 'prize_collected': 306.3730702170471, 'objective': -269.1429469525681}
> Jaccard dist.: 0.11428571428571428
> Hamming dist.: 0.9559659090909091
Lambda = 4.0
> Obj. sample 1: {'edge_cost': 25.06505287957105, 'prize_collected': 226.7623826795313, 'objective': -201.69732979996024}
> Obj. sample 2: {'edge_cost': 37.23012326447901, 'prize_collected': 306.3730702170471, 'objective': -269.1429469525681}
> Jaccard dist.: 0.11428571428571428
> Hamming dist.: 0.9559659090909091
Lambda = 5.0
> Obj. sample 1: {'edge_cost': 25.06505287957105, 'prize_collected': 226.7623826795313, 'objective': -201.69732979996024}
> Obj. sample 2: {'edge_cost': 41.6153825760545, 'prize_collected': 306.3730702170471, 'objective': -264.7576876409926}
> Jaccard dist.: 0.11764705882352941
> Hamming dist.: 0.9573863636363636
Lambda = 10.0
> Obj. sample 1: {'edge_cost': 29.873970790503922, 'prize_collected': 209.45160128136507, 'objective': -179.57763049086114}
> Obj. sample 2: {'edge_cost': 11.773022910393657, 'prize_collected': 205.71245009237012, 'objective': -193.93942718197647}
> Jaccard dist.: 0.2
> Hamming dist.: 0.9772727272727273
Lambda = 15.0
> Obj. sample 1: {'edge_cost': 5.876474987352459, 'prize_collected': 123.35287700024452, 'objective': -117.47640201289207}
> Obj. sample 2: {'edge_cost': 12.990982215735158, 'prize_collected': 182.45966655838677, 'objective': -169.4686843426516}
> Jaccard dist.: 0.0
> Hamming dist.: 0.9815340909090909
Lambda = 20.0
> Obj. sample 1: {'edge_cost': 1.5234903706826128, 'prize_collected': 88.96918230765598, 'objective': -87.44569193697338}
> Obj. sample 2: {'edge_cost': 5.680730602469671, 'prize_collected': 141.21595993438885, 'objective': -135.53522933191917}
> Jaccard dist.: 0.0
> Hamming dist.: 0.9886363636363636
Lambda = 25.0
> Obj. sample 1: {'edge_cost': 1.5234903706826128, 'prize_collected': 88.96918230765598, 'objective': -87.44569193697338}
> Obj. sample 2: {'edge_cost': 2.4332735323262424, 'prize_collected': 96.91390245614741, 'objective': -94.48062892382117}
> Jaccard dist.: 0.0
> Hamming dist.: 0.9914772727272727
Lambda = 30.0
> Obj. sample 1: {'edge_cost': 1.5234903706826128, 'prize_collected': 88.96918230765598, 'objective': -87.44569193697338}
> Obj. sample 2: {'edge_cost': 2.4332735323262424, 'prize_collected': 96.91390245614741, 'objective': -94.48062892382117}
> Jaccard dist.: 0.0
> Hamming dist.: 0.9914772727272727
import pandas as pd
import matplotlib.pyplot as plt
fig, axs = plt.subplots(1, 3, figsize=(12, 4))
df_r = pd.DataFrame(results, columns=["lambda", "obj1", "obj2", "jaccard", "hamming", "union_size", "size_s0", "size_s1"])
df_r["total_obj"] = df_r["obj1"] + df_r["obj2"]
df_r.plot(x="lambda", y="hamming", ax=axs[0])
df_r.plot(x="lambda", y="jaccard", secondary_y=True, ax=axs[0])
df_r.plot(x="lambda", y=["union_size", "size_s0", "size_s1"], ax=axs[1])
df_r.plot(x="lambda", y=["obj1", "obj2"], ax=axs[2])
plt.tight_layout()
# Compare total objective for the two samples vs jaccard distance
# NOTE: Lower values are better, since the problem is framed as a minimization
df_r.plot(x="total_obj", y="jaccard")
<Axes: xlabel='total_obj'>